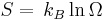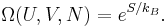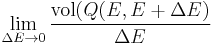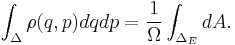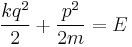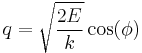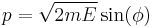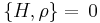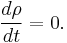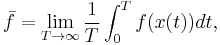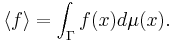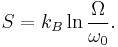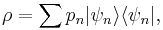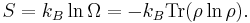Microcanonical ensemble
| Statistical mechanics |
|---|
| Thermodynamics · Kinetic theory |
In statistical physics, the microcanonical ensemble is a theoretical tool used to describe the thermodynamic properties of an isolated system. In such a system, the possible macrostates of the system all have the same energy and the probability for the system to be in any given microstate is the same. It is also called the NVE ensemble because it describes a system with a fixed number of particles 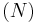 , a fixed volume
, a fixed volume 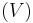 , and a fixed energy
, and a fixed energy 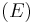 .[1][2]
.[1][2]
Contents |
Terminology
The microcanonical ensemble is a specific instance of a more general construct, the statistical ensemble, a theoretical tool used to analyze macroscopic systems. A given ensemble provides a complete description of all of the possible states of the system. The microcanonical ensemble is distinguished from other ensembles by the fact that the variables that are held constant among all microstates are the number of particles (N), the volume (V), and the total energy (E).
The ensemble is composed of a set of microstates. Each microstate is a complete description of a possible state of the system. In classical mechanics, the microstates of a gas would be represented by the position and momentum of all of the molecules, which in principle specifies all possible degrees of freedom. In quantum mechanics, a microstate would be the composite and complete many-particle wavefunction.
In classical statistical mechanics it is impossible to determine the microstates of the system because all properties of the system are continuous, not discrete. This issue is resolved in quantum mechanics via the use of eigenstates, which are discrete. However, the ensemble approach bypasses these by bundling all microstates that lead to the same macroscopic properties such as volume, temperature or energy in a macrostate.
A statistical ensemble describes this macrostate in terms of all of its microstates. The fundamental postulate of statistical mechanics states that all equal energy microstates of a system are equiprobable. To fully describe a statistical ensemble it is also necessary to specify the probability for a certain microstate to occur, so this postulate circumvents that issue. Thermodynamic properties of the system are then obtained by taking the average value of all microstates in the ensemble.
The Microcanonical Ensemble
In the microcanonical ensemble, all copies of the system have the same number of particles (N), the same volume (V) and the same energy (E). This is precisely what distinguishes an isolated system. If  is the number of accessible microstates, the probability that a system chosen at random from the ensemble would be in a given microstate is simply
is the number of accessible microstates, the probability that a system chosen at random from the ensemble would be in a given microstate is simply 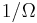 . It is possible to approximately calculate
. It is possible to approximately calculate  for a number of systems such as the ideal gas, the 2-state paramagnet, and the Einstein Solid.
for a number of systems such as the ideal gas, the 2-state paramagnet, and the Einstein Solid.
The benefit of the ensemble is that it allows for calculation of average values for thermodynamic properties. For example, while the pressure of a container of gas fluctuates continuously, we measure the time average of the pressure. The ensemble contains all microstates which the system might inhabit during the period of measurement, so we can replace the time average with an average over the ensemble. Systems for which this is possible are called ergodic.
Relation to the Canonical Ensemble
A canonical ensemble is a distribution over microcanonical ensembles; while in the microcanonical ensemble, the total energy is fixed, the canonical ensemble has only its average energy fixed -- it may exchange energy with a larger reservoir.
Entropy
From the number of accessible microstates,  , we can obtain the Entropy of the system via
, we can obtain the Entropy of the system via
where 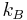 is the Boltzmann constant. Or, equivalently,
is the Boltzmann constant. Or, equivalently,
Some textbooks present this formula as the definition of entropy. If the entropy is defined phenomenologically via the second law of thermodynamics one has to show that the formula above indeed satisfies the law 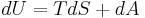 .
.
Notice that, for the microcanonical ensemble,  plays the role of the partition function in the canonical and grand canonical ensembles. For this reason, it is also sometimes referred to as the "microcanonical partition function". We should note here that the notion of multiplicity
plays the role of the partition function in the canonical and grand canonical ensembles. For this reason, it is also sometimes referred to as the "microcanonical partition function". We should note here that the notion of multiplicity 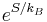 is valid for any thermodynamical system. The same can be said for partition functions and any ensemble. It is only for the microcanonical ensemble that they happen to be the same.
is valid for any thermodynamical system. The same can be said for partition functions and any ensemble. It is only for the microcanonical ensemble that they happen to be the same.
 is also called the characteristic state function of the microcanonical ensemble.
is also called the characteristic state function of the microcanonical ensemble.
An application: residual entropy
The expression for entropy above can be used to calculate the residual entropy.
The third law of thermodynamics says that the entropy of a pure crystalline substance at 0 K is zero. However, in some solids, at temperatures close to 0 K, there may be many molecular orientations. For example, water molecules in ice crystal may arrange themselves in several different ways. In principle, there must be one molecular orientation with the lowest energy. But due to the near randomness with which configurations occur, it is often impractical to attempt realization of the lowest energy configuration. This leads to the notion of residual entropy. Furthermore, there is often very little difference between the total energy of the system and different molecular configurations. Therefore, as an approximation, the system can be viewed having fixed energy and the possible configurations as microstates: a microcanonical ensemble. So it is sensible to estimate the residual entropy via the same expression for the microcanonical ensemble entropy:
where Ω is the number of possible molecular arrangements of the crystal, at some suitable temperature range close to 0 K.
Classical mechanical systems
As with any ensemble of classical systems, we would like to find a corresponding probability measure on the phase space "M". This constant energy assumption means that every system in the ensemble is confined to a submanifold of phase space of constant energy "E". Call this submanifold 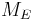 . From the physical considerations given above, it is already clear what the probability measure on the constant energy surface ("not the full phase space") should be: namely, the trivial one that is constant everywhere. However, while only the submanifold
. From the physical considerations given above, it is already clear what the probability measure on the constant energy surface ("not the full phase space") should be: namely, the trivial one that is constant everywhere. However, while only the submanifold 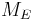 is of interest for the microcanonical ensemble, in other, more general ensembles, it is necessary to consider the full phase space. We now construct a measure on the full phase space that is suitable for the microcanonical ensemble.
is of interest for the microcanonical ensemble, in other, more general ensembles, it is necessary to consider the full phase space. We now construct a measure on the full phase space that is suitable for the microcanonical ensemble.
The Liouville measure 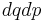 on the full phase space induces a measure
on the full phase space induces a measure 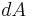 on
on 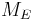 in the following manner:
in the following manner:
The measure of an open subset R of 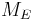 is given by
is given by
Where Q is any open subset of M such that 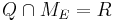 , Q(E, E + ΔE) is part of Q with E < H < E + ΔE, and "
, Q(E, E + ΔE) is part of Q with E < H < E + ΔE, and "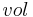 " is the usual Liouville volume. Thus any sufficiently good (measurable) subset of
" is the usual Liouville volume. Thus any sufficiently good (measurable) subset of 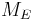 can be characterized by its hyperarea(measure) with respect to
can be characterized by its hyperarea(measure) with respect to 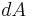 .
.
The density function on the full phase space 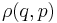 is the generalized function
is the generalized function 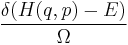 , where H is the Hamiltonian and
, where H is the Hamiltonian and  is the hyperarea of
is the hyperarea of 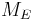 . If Δ is a region of the phase space, the probability of a system being in a state within Δ is simply
. If Δ is a region of the phase space, the probability of a system being in a state within Δ is simply
where 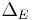 is the intersection of
is the intersection of 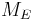 and
and  .
.
Notice how one can either consider the whole phase space and use the measure whose density is a generalized function, or restrict to the constant energy surface in question and use the measure whose density is a constant function. For instance, consider a 1-dimensional harmonic oscillator. The phase space is 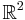 (the position-momentum plane) and the constant energy hypersurface is the ellipse
(the position-momentum plane) and the constant energy hypersurface is the ellipse
The latter can be parametrized as
where  varies between 0 and
varies between 0 and 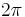 . The measure
. The measure 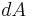 would then equal
would then equal 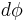 up to a constant. On the other hand, if one considers the ellipse embedded in the plane, then it would have measure zero, which is why a generalized function is used as the density.
up to a constant. On the other hand, if one considers the ellipse embedded in the plane, then it would have measure zero, which is why a generalized function is used as the density.
Connection with Liouville's theorem
We have
(the curly bracket is Poisson bracket) since  is a function of H. Therefore, according to Liouville's theorem (Hamiltonian) we get
is a function of H. Therefore, according to Liouville's theorem (Hamiltonian) we get
In particular, 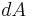 is time-invariant, that is, the ensemble is a stationary one.
is time-invariant, that is, the ensemble is a stationary one.
Alternatively, one can say that since the Liouville measure is invariant under the Hamiltonian flow, so is the measure 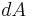 .
.
Physically speaking, this means the local density of a region of representative points in phase space is invariant, as viewed by an observer moving along with the systems.
Ergodic hypothesis
A microcanonical ensemble of classical systems provides a natural setting to consider the ergodic hypothesis, that is, the long time average coincides with the ensemble average. More precisely put, an observable is a real valued function f on the phase space Γ that is integrable with respect to the microcanonical ensemble measure μ. Let 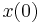 denote a representative point in the phase space, and
denote a representative point in the phase space, and 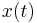 be its image under the Hamiltonian flow at time t. The time average of f is defined to be
be its image under the Hamiltonian flow at time t. The time average of f is defined to be
provided that this limit exists μ-almost everywhere. The ensemble average is
The system is said to be ergodic if they are equal.
Using the fact that μ is preserved by the Hamiltonian flow, we can show that indeed the time average exists for all observables. Whether classical mechanical flows on constant energy surfaces is in general ergodic is unknown at this time.
Remark
The relationship between the microcanonical ensemble, Liouville's theorem, and ergodic hypothesis can be summarized as follows: The key assumption of a microcanonical ensemble is that all accessible microstates are equally probable. Therefore the density function on the relevant region of phase space is constant, say it is 1 everywhere, i.e. the phase space measure μ is just the Lebesgue measure. But, according to Liouville's theorem, this measure is invariant under the Hamiltonian time evolution. From this follows that the notion of time average makes sense for all observables. The ensemble average is defined using μ. The question of ergodicity is whether they coincide. It should perhaps be emphasized that while the microcanonical ensemble and Liouville's theorem are directly related, they should not be confused as being equivalent to the ergodic hypothesis.
Quantum mechanical systems
Semi-classical treatment
So far, we have assumed the system in question is classical. Slight modification is required for quantum mechanical systems, although the results are essentially the same. For an ensemble consisting of quantum mechanical systems, it no longer makes sense to speak of all members of the ensemble having the same definite energy E. So, instead of a level set 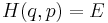 in the phase space, one considers a small range of energies
in the phase space, one considers a small range of energies 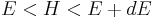 that a system in the ensemble may have and the corresponding region of the phase space. When classical states are replaced by quantum states, the degeneracy needs to be taken into account. Also, in the quantum mechanical case, due to the uncertainty principle, the states can no longer be viewed as continuously distributed in the phase space. Rather, one must find a "fundamental volume"
that a system in the ensemble may have and the corresponding region of the phase space. When classical states are replaced by quantum states, the degeneracy needs to be taken into account. Also, in the quantum mechanical case, due to the uncertainty principle, the states can no longer be viewed as continuously distributed in the phase space. Rather, one must find a "fundamental volume" 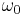 , which depends on the particulars of a given system. As we would expect,
, which depends on the particulars of a given system. As we would expect, 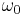 is usually related to
is usually related to 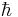 in some way. Consequently, the multiplicity is not the total available volume of the phase space
in some way. Consequently, the multiplicity is not the total available volume of the phase space  but is replaced by
but is replaced by 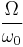 , and entropy becomes
, and entropy becomes
Density operators
The microcanonical ensemble can also be described by a density operator. Namely, if  is the total number of accessible microstates of the system, and
is the total number of accessible microstates of the system, and 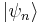 are all states of the system (accessible and otherwise), then a microcanonical ensemble is the mixed state
are all states of the system (accessible and otherwise), then a microcanonical ensemble is the mixed state
where 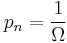 if
if 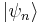 is an accessible state and 0 otherwise.
is an accessible state and 0 otherwise.
We note here that, in this context,  is computed quantum-mechanically, taking into account indistinguishability of particles. The entropy is
is computed quantum-mechanically, taking into account indistinguishability of particles. The entropy is
When 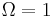 , the ensemble is said to be a pure ensemble. The fact that the entropy vanishes for pure states is essentially the third law of thermodynamics.
, the ensemble is said to be a pure ensemble. The fact that the entropy vanishes for pure states is essentially the third law of thermodynamics.
References
- Raj Pathria, Statistical Mechanics, Elsevier 2001.
|
||||||||||||||||||||||||||